Arc Length by Simpson’s Rule
Simpson’s Rule is a classical numerical integration technique used to approximate definite integrals, especially when the integrand is difficult or impossible to integrate analytically. While it is a fundamental tool in numerical analysis and calculus, its use in machine learning and AI remains relatively niche. Some potential applications include:
Approximating integrals in loss functions (e.g., Bayesian inference and probabilistic models)
Curve length estimation in trajectory-based or path-planning models
Computational neuroscience, for time-accurate modelling of continuous neural processes
Physics-informed machine learning, where physical laws expressed as integrals require numerical approximation
Simpson’s Rule is less common in mainstream machine learning because most models operate on discrete data points and rely heavily on gradient-based optimization methods such as gradient descent, which require differentiable operations. Probabilistic models often prefer Monte Carlo sampling or variational methods over deterministic numerical quadrature like Simpson’s Rule for integral approximation. Additionally, Simpson’s Rule itself is not inherently differentiable, limiting its direct applicability within backpropagation-based training frameworks.
Below is a simple implementation of Simpson’s Rule. It is fast, involves no library overhead, and offers low error (depending on ). It performs especially well on smooth curves with smaller , particularly when the function being integrated is cheap to evaluate.
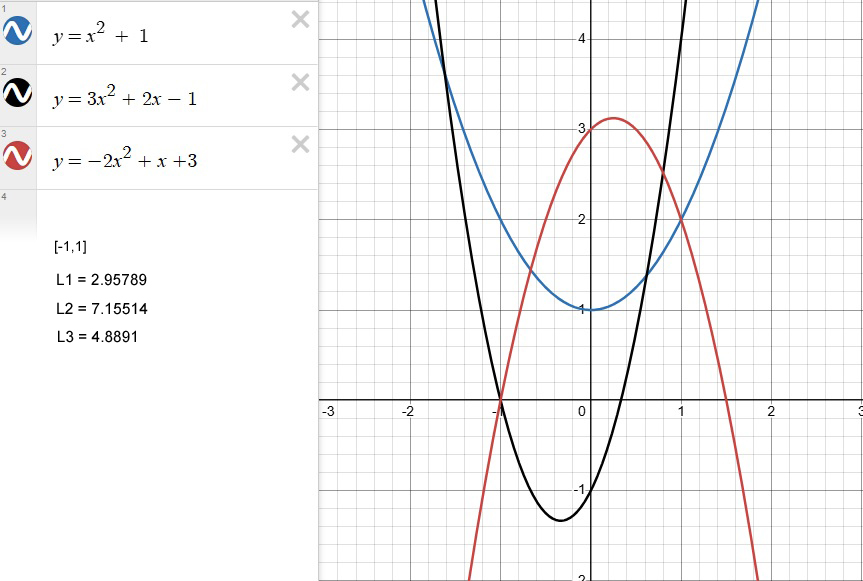
Here, the example functions within [-1,1] (100 sub-intervals) are:
- y = x^2 + 1
- y = 3x^2 + 2x – 1
- y = -2x^2 + x + 3
#include <iostream>
#include <cmath>
template<typename IntegralFunction>
double GetApproximateCurveLength
(const int n, const double a, const double b, IntegralFunction f)
{
// Applying Simpson rule to get approximate curve length
const double deltaX = (b - a) / n;
double totalValue = f(a); // First value in the chain
for(int i = 1; i < n; ++i)
{
totalValue += 2.0f * (1 + i % 2) * f(a + deltaX * i);
}
totalValue += f(b); // Last value in the chain
return (deltaX / 3.0f) * totalValue;
}
int main()
{
// n must be even; a and b define the integration limits
const int n = 100;
const double a = -1.0, b = 1.0;
// y = x^2 + 1
// Integrand for arc length: f(x) = sqrt(4x^2 + 1)
auto IntegralFunctionA = [](double x) { return std::sqrt(4.0 * x * x + 1.0); };
std::cout << GetApproximateCurveLength(n, a, b, IntegralFunctionA) << std::endl;
// y = 3x^2 + 2x - 1
// Integrand: f(x) = sqrt(36x^2 + 24x + 5)
auto IntegralFunctionB = [](double x) { return std::sqrt(36.0f * x * x + 24 * x + 5); };
std::cout << GetApproximateCurveLength(n, a, b, IntegralFunctionB) << std::endl;
// y = -2x^2 + x + 3
// Integrand: f(x) = sqrt(16x^2 - 8x + 2)
auto IntegralFunctionC = [](double x) { return std::sqrt(16.0f * x * x - 8 * x + 2); };
std::cout << GetApproximateCurveLength(n, a, b, IntegralFunctionC) << std::endl;
return 0;
}