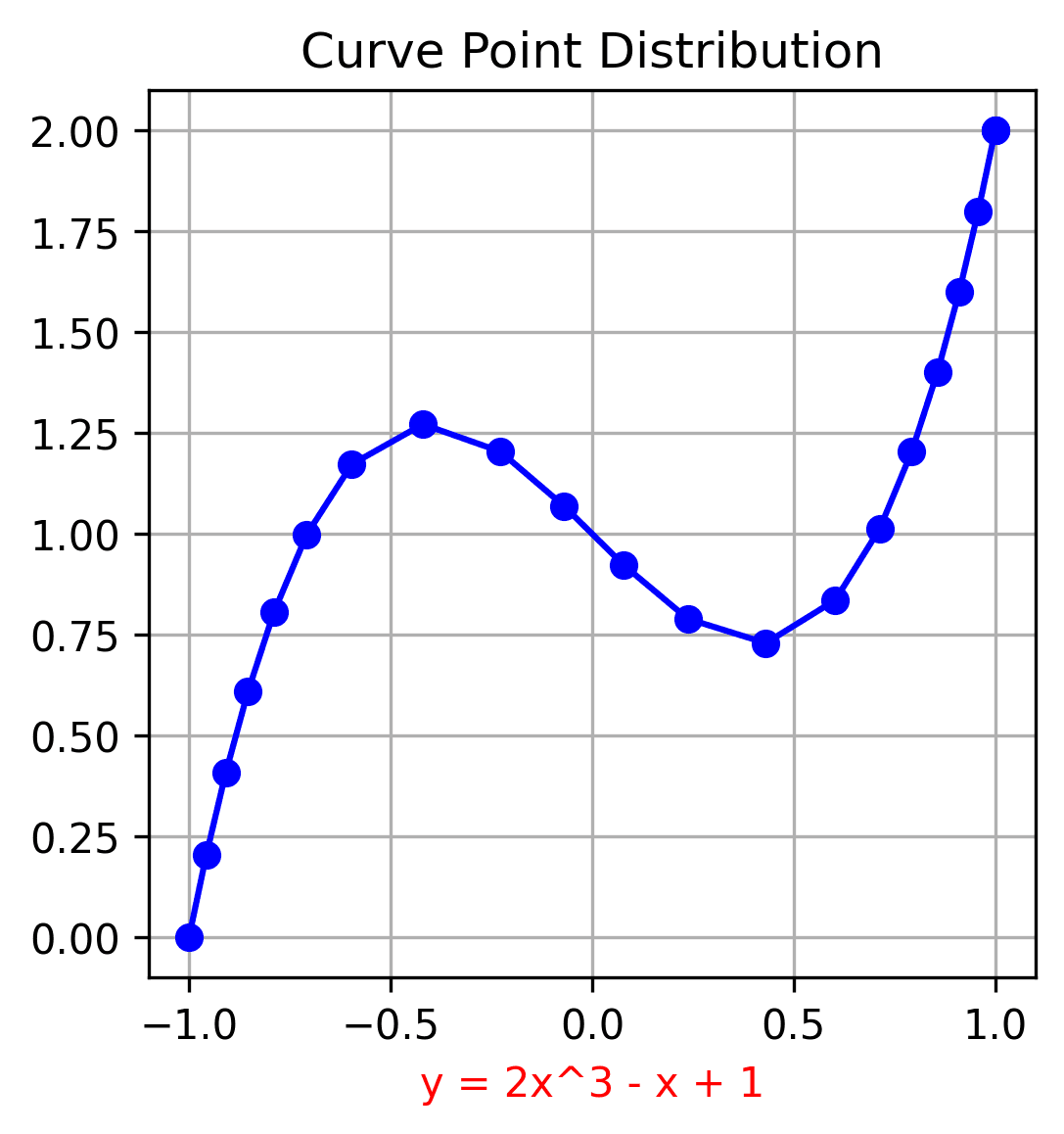
Curve Point Distribution
Python. This implementation’s purpose is to distribute a desired number of points on the curve by equal path distance to each other. To do that, I applied an adaptable unit length strategy while trying to keep the segment length error percent is less than 1% by sweeping small increments on x axis . Later on, I will work on some improvements to reduce errors.
Here, I chose the curve function y = 2x^3 – x + 1 within [-1, 1] range by 20 points and 0.001 delta_x:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 | import numpy as np from scipy.integrate import quad import matplotlib.pyplot as plt class Point: def __init__(self, _x, _y): self.x = _x self.y = _y def function(x): # Taking quadratic function y = 2x^3 - x + 1 as an example return 2 * x**3 - x + 1 def integrand(x): return np.sqrt(36 * x**4 - 12 * x**2 + 2) def curve_Length(a, b): curveLength, _ = quad(integrand, a, b) return curveLength def calculate_Curve_Points(numPoints, deltaX, a, b): curvePointCoordinates = [] # First point as a reference start (lower bound) x = a y = function(x) curvePointCoordinates.append(Point(x, y)) # Sweeping from lower bound to upper bound to get x axis value # First and last point calculations are excluded for k in range(numPoints - 1): delta_x = deltaX lowerBound = curvePointCoordinates[k].x # Adaptable unit length after each error margin unitLength = curve_Length(lowerBound, b) / (numPoints - 1 - k) while True: upperBound = lowerBound + delta_x segmentLength = curve_Length(lowerBound, upperBound) # Error percentage error = 100 * abs(unitLength - segmentLength) / unitLength if error <= 0.1 or segmentLength >= unitLength: x = upperBound y = function(x) curvePointCoordinates.append(Point(x, y)) print("The error of segment", k+1,":", round(error, 2), "%") break delta_x += deltaX # Last point x = b y = function(x) curvePointCoordinates.append(Point(x, y)) # Extract x and y coordinates from curve_point_coordinates x_coords = [point.x for point in curvePointCoordinates] y_coords = [point.y for point in curvePointCoordinates] # Plot the curve plt.figure(dpi=300) plt.plot(x_coords, y_coords, marker='o', linestyle='-', color='b') plt.title('Curve Point Distribution') plt.xlabel('y = 2x^3 - x + 1', color='r') plt.grid(True) plt.gca().set_aspect('equal', adjustable='box') # Set equal aspect ratio plt.show() return if __name__ == "__main__": numPoints = 20 deltaX = 0.001 a = -1.0 # lower bound b = 1.0 # upper bound calculate_Curve_Points(numPoints, deltaX, a, b) |
