Top Cut of Convex Hull

C++. I developed an algorithm based on “three penny algorithm” to find the top cut of a convex hull for dense circle shaped data. It takes the most left point as an entry point like Jarvis’s march. However, it is different from Graham scan and Jarvis’s march because it does its calculation by directly sweeping x plane from left to right.

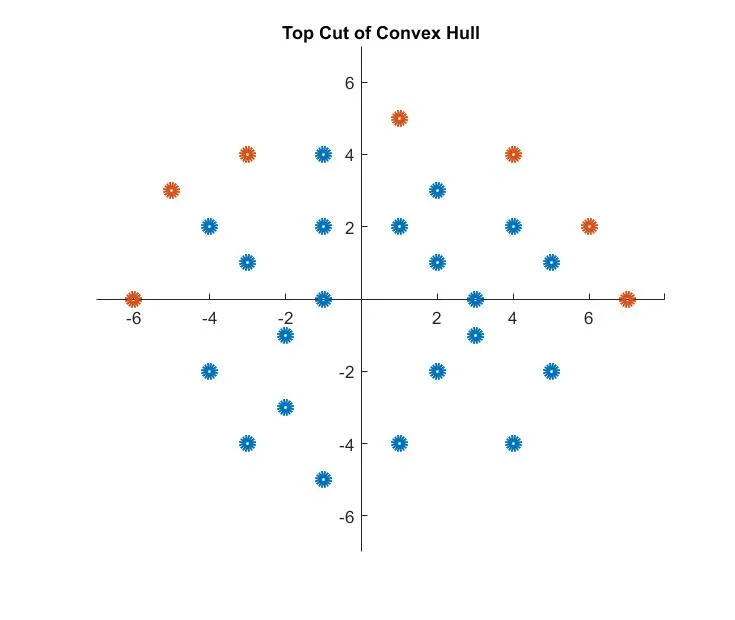
It works with data as sorted and no far extreme points. For extreme points, orientation calculation would change according the position. And also, this algorithm would work for bottom cut too when orientation direction is changed. Moreover, data includes start and end points on x plane for a better demonstration. You will see the circumference points as red on x-y coordinates (see the figure below).

* int data type was chosen for a better readability.

#include <iostream>
#include <vector>
 
struct Point 
{
    int x, y;
    Point(int _x, int _y) : x(_x), y(_y) {}
};
 
std::vector<Point> removeInteriorPoints(const std::vector<Point>& points) 
{
    std::vector<Point> result;
    
    if (points.size() < 3) return result;
 
    result.push_back(points[0]);
    result.push_back(points[1]);
 
    for (int i = 2; i < points.size(); ++i) 
    {
        int size = result.size();
        
        int value = (result[size - 1].y - result[size - 2].y) * (points[i].x - result[size - 1].x) 
                  - (result[size - 1].x - result[size - 2].x) * (points[i].y - result[size - 1].y);
 
        if (value >= 0) 
        {
            result.push_back(points[i]);
        } 
        else if (value < 0 && points[i].x == points.back().x) 
        {
            result.push_back(points[i]);
        } 
        else 
        {
            while (value < 0) 
            {
                result.pop_back();
                size = result.size();
                
                value = (result[size - 1].y - result[size - 2].y) * (points[i].x - result[size - 1].x) 
                      - (result[size - 1].x - result[size - 2].x) * (points[i].y - result[size - 1].y);
 
                if (value >= 0 || size == 1) 
                {
                    result.push_back(points[i]);
                }
            }
        }
    }
 
    return result;
}
 
int main() {
    // dense circle shape sorted data at x-y coordinates
    // it does not include extreme points affecting the circle area density
    std::vector<Point> dataSet = {
        { -6,0 },{ -5,3 },{ -4,-2 },{ -4,2 },{ -3,-4 },{ -3,1 },{ -3,4 },{ -2,-3 },
        { -2,-1 },{ -1,-5 },{ -1,0 },{ -1,2 },{ -1,4 },{ 1,-4 },{ 1,2 },{ 1,5 },
        { 2,-2 },{ 2,1 },{ 2,3 },{ 3,-1 },{ 3,0 },{ 4,-4 },{ 4,2 },{ 4,4 },
        { 5,-2 },{ 5,1 },{ 6,2 },{ 7,0 }
    };
 
    // Remove interior points
    std::vector<Point> result = removeInteriorPoints(dataSet);
 
    // Print result
    for (const Point & p : result) 
    {
        std::cout << "(" << p.x << "," << p.y << ")" << std::endl;
    }
 
    return 0;
}

References:

[1] Convex hulls

[2] Convex hull Jarvis’s Algorithm